 |
 |
■■■
■■
■ dbookProはいい!
昨日の続き,三角形の内角の和を証明。
言葉でのやりとりで説明できることと,
証明が書けることの差は大きい。
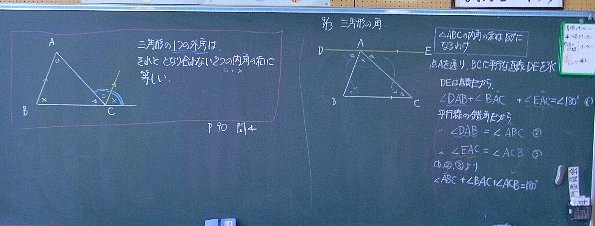
とはいえここまで,図形の証明を,
スタンドアップのやりとりで,よくやっている。
・対頂角 ・平行線の錯角 ・同側内角の和
まとめのプリントを作ろうかと思う。
マグネットスクリーンを使うと,板書スペースが不足する。
今回も,右から左へ進む板書になってしまった。
Mimioで書いたり動かしたりをしたいので,
マグネットスクリーンを使ったためにこうなってしまったのだが,
結局,サイドの吊ったスクリーンで。
Mimioではボタン操作でも,
空中でも書いたりつかんで動かしたりができるのだがら,
練習してできるようにしなくては。

昨日同様,小学校で学んだことを引き出して,
三角形の内角の和が180度になることを証明する授業。
このクラスでは,紙を折ることも生徒から出てきた。
dbookPROで小学校の教科書を提示。
電子教科書化する操作がとてもシンプルで,
ほとんどマニュアルなしでも出来てしまうのはありがたい。
マニュアルを読むと,さらに痒いところに手が届く仕様も。
自分専用の電子黒板が欲しくなってきた。
2006年09月13日(水) 意図を理解させた上で
2005年09月13日(火) 光が見えてこない
2004年09月13日(月) ちょっと前進
2011年09月13日(火)
|
|
 |