 |
 |
■■■
■■
■ 優れた問いを理解できない
方程式と等式の違いの授業を2つ。
高校生でも正しき答えられる生徒は少ないことだろう。
これを授業で扱う面白さは、
感じられる生徒はどのぐらいいるのか・・・。
最初のクラスでは、生徒の問い「2χ+3=2χならどうなる?」
を生かしたもの。
これは、前回の授業での結論、
「右辺と左辺のχ係数が違うから、解は一つしかない」
を受け手の優れた問い。
しかし、前段階の部分も、この問いの意味も理解できる生徒は少なく、
授業としては共有化が難しい。

*板書は左半面からスタート。
スクリーンをはずした右半面が後半の内容。
方程式の定義を示して、方程式でないものを提示したこの授業の方が
多くの生徒にとってはこの目標を達成できたと思う。

教師にとっては面白い授業ではないのだけれど。
後半は、方程式を解くもの。
ゴールのイメージから、解く方向性を示す。
移項についての解説。
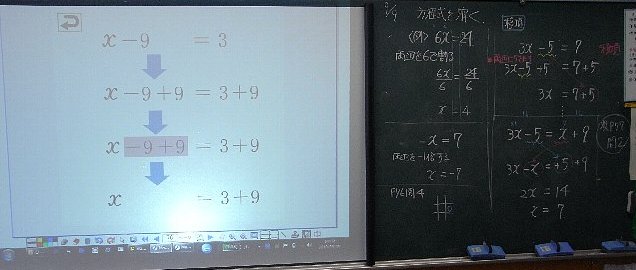
まずは、黒板に書いて生徒にもノートに書かせ、
そこから、移項を示す。
さらにスクリーンでその違いを確認する。
何度も見せることができるのがいいように思って見せていたが、
この場面ではデジMATHを使うことは今ひとつなのかもしれない。
書くことの方が、生徒の意識には残るのかも。
2006年09月09日(土) 磨いてくださる方がいるから
2005年09月09日(金) ちょっと違った感じ
2004年09月09日(木) 疲れを感じつつも
2010年09月09日(木)
|
|
 |