 |
|
■■■
■■
■ 問いの連鎖が始まる
２つの正三角形の問題の続き
基本的な問題を解いた後は，生徒の問いを紹介していく。
これまで、授業の振り返りカードでは、
どんな内容でも問いが書いてあれば、「次がある」にチェックを。
その問いがよければ「問いがgood」にチェックし
全体の場で紹介させてきたが、
実際は、なかなかチェックを付け難かった。
そこで、その中間を作ることとした。
紹介したい内容の問いは、
「次がある」のチェックにさらに丸を付けることにした。
久しぶりにネームプレートを活用。
合同な三角形がまだ存在することが見えるのは，
d-book＋GCLでの手書き機能＋移動を見せたからだろう。
対応が見えてくると，合同が見えてくる。
条件（仮定）を変えたらどうなるかという話が，盛り上がる。
二等辺三角形なら・・条件を弛めるいい問いだ。
でもそれだけでは図形を描けない。
その感覚を理解させるには，
作図ツールで作図させることなのだろうが，・・・
直角二等辺三角形や，正方形で考えさせる。
時間の関係から、「追究してみよう」「気がついたことを説明し合おう」
という放り投げる感じの授業に。
わからない生徒もいたことだろう。
でも，こんな自由度もたまにはいいかな。
点Cが線分ではなく直線上を動いたらや、
点Cを線分からはずしたフリーな点にしたら・・・
という問いも出てくる。
わくわくする瞬間。
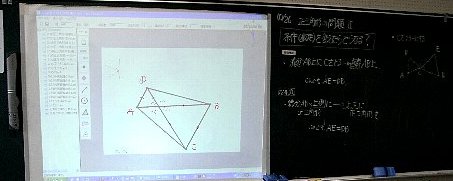
別のクラスでは，一つの三角形を逆にしてみたら・・という問い。
 この方が自然に合同が見えてくる
左右対称な図形。
こんな発想が出てくるのは，
dbookで気軽に図形を対称移動しているからか。
見えてくるものが
違ってきている気がするのはうれしい。
2006年10月26日(木) 相乗効果で
2005年10月26日(水) 自信から確信へ
2004年10月26日(火) 虹は二次曲線!?
2007年10月26日(金)
|
|
|
スタンドアップでの