 |
 |
■■■
■■
■ 待てないということなのか
二乗に比例する関数の授業もそろそろ大詰め。
進んでいるクラスでは,変化の割合が見せる不思議な世界。

一点を中心に範囲を等間隔で狭めていくと,
変化の割合が変らないことを確認。
ここから予測されることや気が付いたことを待つ。
なかなか出てこない中,顔つきから2人を指名。
出されたことは,
・χの範囲となる両端の数の和が,変化の割合に等しい
・グラフにしたら,平行線が表れること
まずまずの内容。
本当はもっといろいろ出てくるといいのだけれど,
ここで積極的な意見が出せないのは,授業者の腕か。
さらに,待てなかったのは,
「どうしたらこれを確かめられる?」という発問。
これぞ,数学的な見方考え方というよりも,
科学的な思考力を問う絶好の問題ったと,後から気が付く。
ゴールが多様化していくときどう収束させていくのか,
その場のアレンジ力の未熟さも感じる。
いつもなら,振り返りカードで授業を切って,
生徒の反応を見るところにしているから,
生徒も教師も,こういう積み上げに弱いのか。
とはいえ,今後の反応は楽しみ。
送れているクラスは,またまた授業CUTにはまる。
宿題に対する姿勢を改めて問い,
その後は変化の割合について。
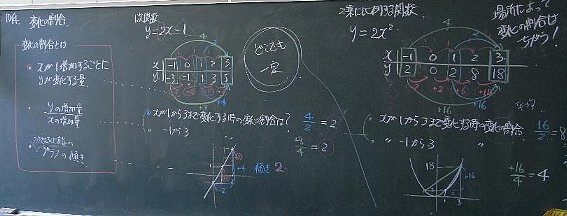
ここで分かってくれると嬉しいのだけれど。
午後は娘の保護者会。
知り合いの先生も何人か。
立場が変ると,いろいろなことが見えてくるもの。
自分の過去も,見えてきて困ったもの。
2007年10月14日(日) 市民大会
2006年10月14日(土) 大会前の練習試合
2005年10月14日(金) 人を動かす難しさ
2004年10月14日(木) 魔法の杖
2009年10月14日(水)
|
|
 |