 |
 |
■■■
■■
■ 意外なところで
平行線と比の問題を再確認。
教科書の問題で復習するぐらいのつもりが,
意外なところで,おもしろい展開に。
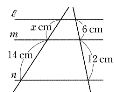 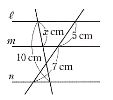
この問題を4人組で。
久しぶりの4人組でも,いい感じのやり取り。
見えている生徒には当たり前の問題でも,
そうでない生徒も当然いる。
この差があるから,いい関わり合いが成立する。
大体できたところで,mimioを使って生徒に書かせてみる。
考えてみれば,mimioを生徒に操作させたことがなかった。
それだけで意欲的な生徒たち。
見ているだけあって,操作自体はよくわかっている。
ちょっと難しい右の問題で,
他の式で考えた生徒を前に出させて書かせると,
実にいろいろなものが出る。
χ:(10−χ)=5:7
χ:10=5:12
ここまでは当たり前。さらに,
χ:5=10−χ:7
χ:5=10:12
などなど。
この発想で,再度左の問題を考えさせてみた。
この発問もなかなかHITする。
相似な三角形では,相似比と構成比があるように,
平行線と比でも,上下の比と,左右の比がある。
いろいろな見方ができることや,
それでも同じ式が導かれることに感動が生まれる。
活躍する生徒が多いのも,やっぱりいい。
最後に,平行線を利用した3等分の作図を紹介。

次回は,紙を3等分する展開へ持ち込む予定。
ここで文字式にして,
a:b=c:d
a:c=b:d
a:a+b=c:c+d
b:a+b=d:c+d
が全て同じになることを確認してもよかった。
これは,またの機会か。
この美しさを,GCなら簡単に数式化して表わせるが,
Voyageでは数式表示が可能なのか?
確かめておこう。
新たな授業構想が生まれ,
折れていた気持ちが少しだけ変わる。
担任が2人不在で,代打。
久しぶりの道徳はドナーカードの2時間目。
保護者の子供に対する思いが,授業を本物にしていく。
また,いつもは授業していないクラスでは,
ボール落下の授業を楽しむ。
2007年12月04日(火) 生徒の問いで進む授業の楽しさ
2005年12月04日(日) 遅めの起床
2004年12月04日(土) 山あり谷あり
2003年12月04日(木) ダウン
2009年12月04日(金)
|
|
 |