 |
 |
■■■
■■
■ 数学的な美しさ
欠席2名,早退4名。気になる情報も。
2乗に比例する関数の授業も,あとわずか。
一番遅いクラスは,ボール落下のまとめ。
わずか30cmの測定で,9mの落下が予測できることは,
グラフで見ると実にすごいことだと実感。
最初の1秒後には,5mほどしか落下しないが,
3秒後には45mも落下するのだということを計算で出す。
これまた実感を持って「すごい」と生徒が感じている。
東京タワーからボールを落としても,8秒程度で地面に着く計算。
変化の割合も,必然性を持って語れるのはいい。
ずいぶん楽しませてもらったが,テストはできるようにしたい。

自分は今まで,早く終わった生徒は多くの問題を解くような授業を考えてきた。
しかし,M先生は違う。
問題は多くても2問ぐらい。
じっくり時間をかけて,全体で発表する前に,生徒同士が教えあって,その中でほとんどの生徒が理解する。
だから,全体での説明はかなりあっさりでいい。
生徒同士の関わりがいいこの学年だからできることかもしれないが,
こういう授業だと,みんなができて,みんながわかる流れになる。
このスタイル,是非とも多くの方に真似してほしい方法だと思う。
できることで生徒のやる気が違ってくる。
うれしそうな笑顔を見られる瞬間も確かにうれしい。
夜も,そのことでM先生と話し合う。
できることを生徒は求めている。
できなくても,そこに不思議が残ってもいいというスタイルは,
たまにはいいのだろうが,できない生徒にとっては,苦痛なだけ。
自分の中の数学観が揺らぐのがわかる。
 また, また,
「単純に美しいというだけでは,本当の数学の美しさとは言えない」
という言葉も,
その通りかもしれない。
これまでの自分は,
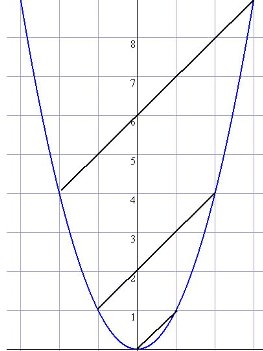
放物線の格子点を斜めに結ぶと平行になる話も,
今までは,単純に美しいことで喜んでいた。
しかし,きちんと数式で計算して,確かに平行になるという話にしてみるからこそ,その美しさ,奥深さが本当に分かるというもの。
Y=aX^2において,Xがbからcまで変化するときの変化の割合は,
(ab^2-ac^2)/(b-c)
=a(b+c)
一方,その一つ内側は
(a(b+1)^2-a(c-1)^2)/(b+1-(c-1))
=a(b+1)+a(c-1)
=a(b+c)
となり等しくなる。
ここまでやって初めて,数学的美しさ・・・そうかもしれないと思う。
もっとも,ついてこれる生徒は少ないだろうが。
2003年11月09日(日) 日記スタート
2004年11月09日(火)
|
|
 |