 |
 |
■■■
■■
■ 分母の有理化で
早いもので,もう7月。
数日欠席していた何人かの生徒が登校。
しかし早退する生徒もいて,
いつも誰かがいないのは気になるもの。
授業は,根号のついた数の有理化。
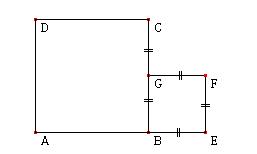
ルートのものさしを使って,
一辺が√2の正方形をかき,
その横に半分の正方形をかく。
それぞれの面積が
2と1/2であることを確認し,
線分AEの長さを問う。
・2つの長さを足して,√2+√1/2
・線分BEは,ABの半分なので,√2+1/2*√2=3/2*√2
・AEを一辺とする正方形をかき,面積は9/2だから,√9/2
そこで,この3つが確かに等しいことを,図以外で考えさせる。
ここまで何回も同様の展開できているので,
難しいけれどわかりやすい授業展開。
単なる計算ではなく,必然性がある流れなのがいい。
平方したり,分母を有利化したり,近似値だったりと,
いろいろなアプローチで迫っていくおもしろさ。
でも,有理化の計算が強く印象には残るわけではない。
指導主事が見れば感心するだろうが,
塾の教師が見れば,ダメだと言うことだろう。
授業のおもしろさと難しさを,改めて感じる。
事件発覚,放課後は対応に追われる。
やや遅れて,市の数学同好会へ。
参加者が少ない。話題提供ということで,
夏期研の実践発表をどうするかを皆さんに聞いていいただく。
GRAPES,U-BASIC,GC,Voyage200を使った,
瞬間芸的なものをたくさん紹介するのか,
それとも「影の長さ」や「数の法則」など
1つの授業に絞って紹介するのがいいのか。
以前の選択でのことも含めて,
1時間ほどの時間で,たくさん聞いていただく。
これだけの時間があると,
おもしろさをご理解いただけるが20分だと難しい。
Voyage操作していただいて・・というのは
やめようと改めて思う。
このところ,ウイルスメールが毎日のように届く。
今はほとんど使っていない,以前のアドレスからのもの。
何のために,こんなことをする人がいるのか。
2004年07月01日(木)
|
|
 |