 |
 |
■■■
■■
■ 選択授業三回目
今日も「√2+√5=√7になるか」を考える授業。
・それぞれを平方すると,2+5=7になる
・近似値で考えるとならない
という両案を授業の前半に出させ,
その上で,再度どちらが正しいのかを考えさせる。
自分の主張を正当化するだけでなく,
相手の主張を否定しなければならないので,
理解が深まる仕組み。
結論を分かっているだけでは,何もできない。
意外な生徒が図解しているのもうれしい限り。
1章で,タイル図にこだわったことが生かされているのかも。
分母の違う分数が,なぜ簡単に足せないのかと,
対比して言い出す生徒がいないのが,ちょっと不思議。
選択授業は三回目。
変化するもの,しないものを分類していく。
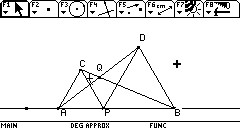
変化するものとして,
△QABや
四角形CPDQが出された。
これは面白そう。
変化しないものについて,
先に扱おうとしているが,
変化するものの方が面白そう。
そうこうしていると変化しないものとして,
∠CQAをかなりの生徒が発見。
しかもこれが60度ということも。
こんなに早く発見されるとは思わなかった。
これを導くため,AD=CBを次回は証明させようと思う。
今回も,スクリーンで見せること,Voyage操作で発見
紙で確認のそれぞれの使い分けが,もう1つ。
また,Voyageの画面が小さいので,
測定を生徒に勝手にさせて発見させるのにはためらいがある。
そう言っているより,やらせたほうが面白いかな。
GC/JAVAを使っていたときには,測定値が図の近く出ないことに
不満を感じていたが,
記号付きで一覧として表示されるよさも見えてくる。
Voyageで,測定値の計算式を表示する方法や,
これを表(CEL)に組み入れる方法を勉強しなければ。
2004年06月22日(火)
|
|
 |