 |
|
■■■
■■
■ 多くの方の支えで
なかなか疲れが取れないのが気になる金曜日。
欠席３人。
授業は，ボールの落下。
この日の朝，金沢高専の三尾さん届いたばかりの改良プログラムは，
なんとバージョン７。
切り取りをやり直せるのはとてもありがたい。
説明20分，実験20分という感じで収まってきた。
とはいえ今日もデータをVoyageに転送する際，エラーがかなり出る。
原因は，おそらく距離センサーCBRの電池切れと，
転送中にケーブルを動かしてしまうこと。
ちょっとしたことでエラーが起きることを確認する。
機器を机においてデータを転送すると，ほとんどエラーは生じない。
授業後，
「先生，今日の授業は特に面白かった。」の声。
Voyage使いの達人になった生徒からは，
「やっと数学らしくなりましたね。」
使える数学になってきたことに，生徒も満足。
 進んでいるわがクラスでは，班ごとの実験の発表。
黒板を斜め上に転がるボールの軌跡
対応表も書いて，
違いのなさを示す。
バウンドするボールの軌跡を追ったグループ。
頂点前は Ｙ＝-0.2Ｘ^2，
頂点後では Ｙ＝-0.22X^2と
若干違いがあったとのこと。
「頂点を取る際の誤差ではないか」
と発表していたが，それは空気抵抗がなせる業かもしれないと思った。
ホームランボールの軌跡も，実はきれいな放物線ではない。
曲線をよく読んでいる生徒たちに関心。
転がるガムテープのグループの動機が，
「加速するもので2乗に比例するのなら，
減速するものでも2乗に比例するのではないか」というものだった。
こういう柔軟な発想を，もっともっと引き出す授業をしたい。
それはテストには出題されないことだけど，
きっと生徒がこれから生きていく中で，使える力になるはず。
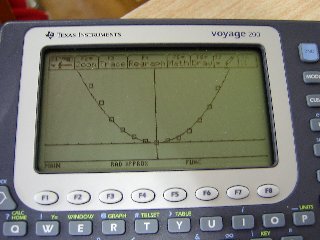
さらに驚いたのは，
下敷きカーブ。
この状態から，一致する二次曲線はなかったと発表する。
確かによく見ると，原点付近では一致するが，
原点から離れるにつれて，数式のカーブはデータの外側に。
比例定数をもう少し大きくすると，
原点付近のカーブに合わないことまで確認していた。
素直に事象を分析できる眼を持っている生徒たち。
大人のほうが，先入観があってダメなのかもしれない。
秋田大の後藤先生や，石川高専の沢田先生からいただいた
これらの事象に関するメールを紹介して終わる。
なんだかとてもアカデミックな気分。
2004年11月05日(金)
|
|
|
