 |
 |
ЂЃЂЃЂЃ
ЂЃЂЃ
ЂЃЁЁЭЅЄьЄПЬфЄЄЄђЭ§ВђЄЧЄЄЪЄЄ
Ъ§ФјМАЄШХљМАЄЮАуЄЄЄЮМјЖШЄђЃВЄФЁЃ
ЙтЙЛРИЄЧЄтРЕЄЗЄХњЄЈЄщЄьЄыРИХЬЄЯОЏЄЪЄЄЄГЄШЄРЄэЄІЁЃ
ЄГЄьЄђМјЖШЄЧАЗЄІЬЬЧђЄЕЄЯЁЂ
ДЖЄИЄщЄьЄыРИХЬЄЯЄЩЄЮЄАЄщЄЄЄЄЄыЄЮЄЋЁІЁІЁІЁЃ
КЧНщЄЮЅЏЅщЅЙЄЧЄЯЁЂРИХЬЄЮЬфЄЄЁжЃВІжЁмЃГЁсЃВІжЄЪЄщЄЩЄІЄЪЄыЁЉЁз
ЄђРИЄЋЄЗЄПЄтЄЮЁЃ
ЄГЄьЄЯЁЂСАВѓЄЮМјЖШЄЧЄЮЗыЯРЁЂ
ЁжБІЪеЄШКИЪеЄЮІжЗИПєЄЌАуЄІЄЋЄщЁЂВђЄЯАьЄФЄЗЄЋЄЪЄЄЁз
ЄђМѕЄБМъЄЮЭЅЄьЄПЬфЄЄЁЃ
ЄЗЄЋЄЗЁЂСАУЪГЌЄЮЩєЪЌЄтЁЂЄГЄЮЬфЄЄЄЮАеЬЃЄтЭ§ВђЄЧЄЄыРИХЬЄЯОЏЄЪЄЏЁЂ
МјЖШЄШЄЗЄЦЄЯЖІЭВНЄЌЦёЄЗЄЄЁЃ

ЁіШФНёЄЯКИШОЬЬЄЋЄщЅЙЅПЁМЅШЁЃ
ЁЁЅЙЅЏЅъЁМЅѓЄђЄЯЄКЄЗЄПБІШОЬЬЄЌИхШОЄЮЦтЭЦЁЃ
Ъ§ФјМАЄЮФъЕСЄђМЈЄЗЄЦЁЂЪ§ФјМАЄЧЄЪЄЄЄтЄЮЄђФѓМЈЄЗЄПЄГЄЮМјЖШЄЮЪ§ЄЌ
ТПЄЏЄЮРИХЬЄЫЄШЄУЄЦЄЯЄГЄЮЬмЩИЄђУЃРЎЄЧЄЄПЄШЛзЄІЁЃ

ЖЕЛеЄЫЄШЄУЄЦЄЯЬЬЧђЄЄМјЖШЄЧЄЯЄЪЄЄЄЮЄРЄБЄьЄЩЁЃ
ИхШОЄЯЁЂЪ§ФјМАЄђВђЄЏЄтЄЮЁЃ
ЅДЁМЅыЄЮЅЄЅсЁМЅИЄЋЄщЁЂВђЄЏЪ§ИўРЄђМЈЄЙЁЃ
АмЙрЄЫЄФЄЄЄЦЄЮВђРтЁЃ
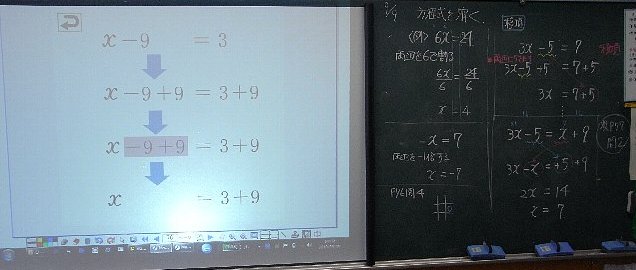
ЄоЄКЄЯЁЂЙѕШФЄЫНёЄЄЄЦРИХЬЄЫЄтЅЮЁМЅШЄЫНёЄЋЄЛЁЂ
ЄНЄГЄЋЄщЁЂАмЙрЄђМЈЄЙЁЃ
ЄЕЄщЄЫЅЙЅЏЅъЁМЅѓЄЧЄНЄЮАуЄЄЄђГЮЧЇЄЙЄыЁЃ
ВПХйЄтИЋЄЛЄыЄГЄШЄЌЄЧЄЄыЄЮЄЌЄЄЄЄЄшЄІЄЫЛзЄУЄЦИЋЄЛЄЦЄЄЄПЄЌЁЂ
ЄГЄЮОьЬЬЄЧЄЯЅЧЅИЃЭЃСЃдЃШЄђЛШЄІЄГЄШЄЯКЃЄвЄШЄФЄЪЄЮЄЋЄтЄЗЄьЄЪЄЄЁЃ
НёЄЏЄГЄШЄЮЪ§ЄЌЁЂРИХЬЄЮАеМБЄЫЄЯЛФЄыЄЮЄЋЄтЁЃ
2006ЧЏ09Зю09Цќ(Хк)ЁЁЫсЄЄЄЦЄЏЄРЄЕЄыЪ§ЄЌЄЄЄыЄЋЄщ
2005ЧЏ09Зю09Цќ(Жт)ЁЁЄСЄчЄУЄШАуЄУЄПДЖЄИ
2004ЧЏ09Зю09Цќ(Ьк)ЁЁШшЄьЄђДЖЄИЄФЄФЄт
2010ЧЏ09Зю09Цќ(Ьк)
|
|
 |