 |
 |
■■■
■■
■ 選択授業4回目
欠席,早退合わせて5名。連絡が取れず気になる生徒も。
授業は,平方根の加法。
一辺が√2の正方形をルートのものさしで作図し,
そのとなりに,一辺が2倍の正方形をかく。
そして,この辺の和を問う。
3√2,√2+√8,√18
の三通りの答え方が出る。
そこで,これらが同じものであることを数式で考えさせる。
ここまでの授業の流れから,
平方して考えたり,ルートの積の法則を持ち出したり,
近似値で等しくなりそうなことに迫ったりと,
多様な考えが出されるのがいい。
最初は,簡単すぎるのではと思っていたが,
生徒にとっては十分問題となりうることを改めて認識。
ルートの数は,なかなか難しいもの。
それを,こうやって授業化しているM先生の力に敬服。
選択授業も4回目。
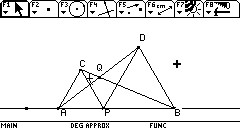 前回問題になった, 前回問題になった,
AD=CBや
∠CQA=60°を,
紙の上で再び確認し,
さらにVoyage200上で,
Pが変化しても変わらないことを
確認する。
おかしなもので,作図ツールでは変化しない方が,
ツールがきちんと働いていないのではと感じてしまう。
まずは,AD=CBの証明を考えさせ,
三角形の合同を利用し,証明しきる。
それを利用して,∠CQA=60°の証明を
考えるところで,時間切れ。
終了後も,黒板の周りに集まって,
なにやら相談している姿がいい。
図形の回転移動を利用した証明が出るとおもしろい。
2004年06月29日(火)
|
|
 |